東北大学加齢医学研究所
心臓病電子医学分野/非臨床試験推進分野
東北大学大学院 医工学研究科
人工臓器医工学講座
東北大学大学院 医学系研究科医科学専攻
心臓病電子医学
人工臓器があなたの身体を治します
人工臓器研究のこれから
頭の先からお尻の先まで、
人工臓器があなたの身体を治します
新しい医療は、東北大から生まれます。
・人工心臓/補助循環/人工心筋
・心臓代用弁
・血管治療/ステント
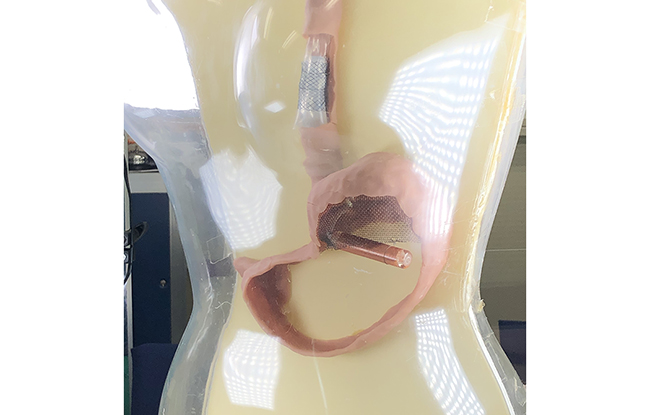
・人工食道/人工括約筋/人口舌
・自律神経/嚥下機能
【技術キーワード】
・循環解析
・モデリング
・非臨床試験
・小児循環器治療シミュレーション
・自律神経機能と血液循環
・生体エネルギー応答・発電
・肺炎予防
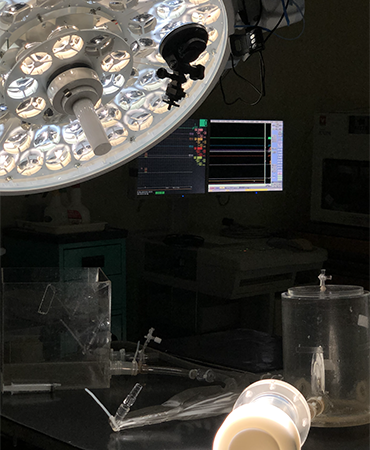
手術室・モデル実験
心臓モデルシミュレーション

血液損傷試験
血液負荷試験

耐久性評価
血液ポンプ耐久試験装置
Research
補助循環システム・
生体臓器機能代替システムの開発
・経皮的補助循環/右心循環補助
・人工心筋
・人工食道/人工括約筋
・人口舌
医療機器の非臨床評価
・血液循環モデリング・シミュレーション
・小児用肺動脈弁開発評価研究
・医療安全/医療機器の安全性評価研究
・人工心肺の評価システム開発
血行動態を制御する自律神経系の影響
・末梢循環の非侵襲解析
・非接触嚥下機能評価
・ドライブシミュレーション
血液損傷メカニズムの研究
・血液剪断負荷試験装置開発
・血液ポンプの血液適合性評価
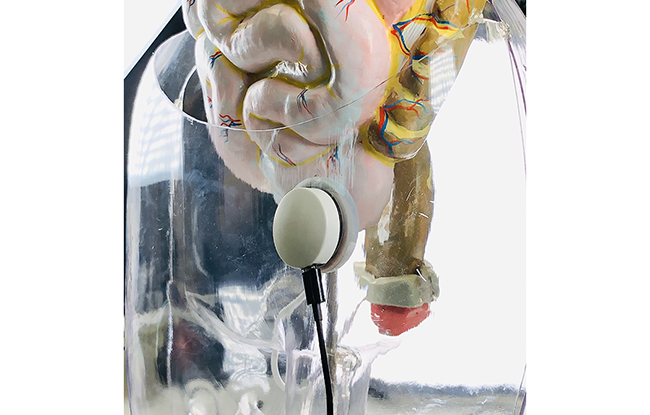
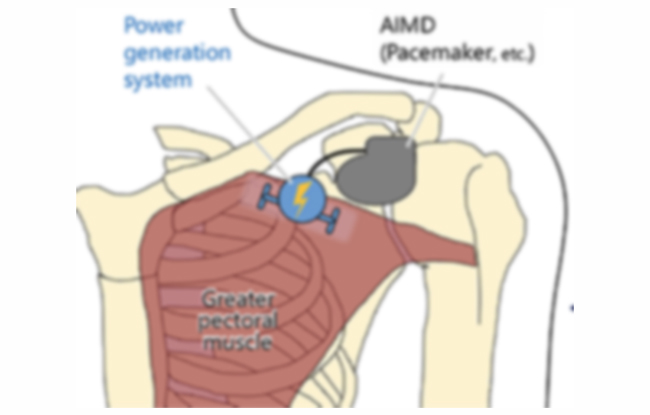
体内でエネルギーを得て、人工臓器で生体機能を代替するシステム
・植込み型医療機器の生体内応答
・人工臓器の生体適合性解析研究
Latest News News in Professor's Facebook
Contact
Fax. 022-717-8518
(〒980-8575)